다양한 Quantization 방법에 대해 소개하고 각각의 방법의 장단점 들을 소개하는 논문이다. Basic concept 부분과 Advanced concept 부분이 있는데 여기서는 basic concept만 다루고 다음 포스팅에서 Advanced concept를 다룰 예정이다.
Abstract와 Introduction 등은 생략하고 Quantization 방법론 위주로 정리해보았다.
III. Basic concpts of Quantization
B. Uniform Quantization

r은 real value(quantizaion 이전의 원래 값) 이고 S는 scaling factor, Z는 integer zero point라고 한다. Int 함수로 S로 나누어진 real value(high-precision) 를 integer value(low-precision)로 매핑하게 되면서 bit수를 줄일 수 있는 것이다. 위의 식을 통해 바꾸면 일정한 r 값의 구간마다 Q(r)을 통해 일정한 값으로 매핑 되기 때문에 Uniform Quantizaion이라고 한다. 이렇게 quantizaion된 값은 아래와 같은 식으로 다시 원래 bit수로 dequantizaion 될 수 있다.

여기서 다시 dequantizaion 된 값은 오차 때문에 원래의 real value값과 정확하게 같지는 않을 수 있다.
C. Symmetric and Asymmetric Quantizaion
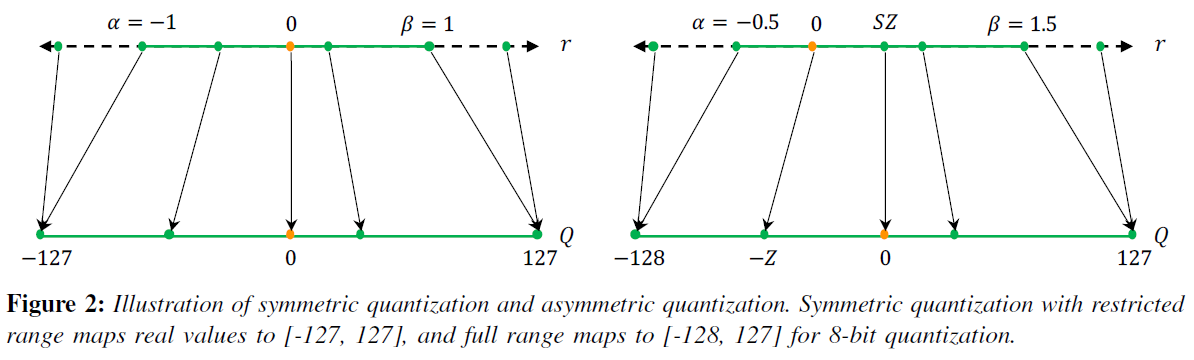
위의 그림에서 $\alpha$ 와 $\beta$는 clipping range를 정해준다. clipping range는 quantization을 적용할 real value 값의 범위이다. 이 $\alpha$와 $\beta$가 0을 기준으로 symmetric하게 설정이 되면 symmetric quantization이고 아니면 asymetric quantizaion이다. 이러한 clipping range를 정하는 과정을 calibration이라고 한다.
직관적인 방법으로는 r의 최솟값을 $\alpha$로 설정하고 r의 최댓값을 $\beta$로 설정하면 모든 real value의 범위를 quantizaion에 적용할 수 있어서 편해 보이지만 그러면 symmetric하게 설정이 되지 않는다.
인기 있는 방법 중 하나로 아래와 같은 방식으로 $\alpha$와 $\beta$를 정하는 방법도 있다.

Asymmetric quantizaion방법도 필요한 상황이 있는데 weight나 activation 값들이 imbalance할 때이다. 예를 들어 ReLU 같은 activation을 통과하면 음수는 모두 0이 되므로 asymmetric 방식을 적용해야 한다.
그림 3에서 볼 수 있듯이 symmetric 방식은 0을 0으로 mapping 하는데 비해 asymmetric 방식은 0을 0으로 매핑하지 않는다. 이것은 연산량 관점이나 implementation 관점에서 꽤 차이를 만들 수 있어서 symmetric 방식이 선호 되는 이유 중 하나이다.
또한 $\alpha$와 $\beta$를 단순 real value의 min이나 max로 정하면 outlier 의 영향을 많이 받을 수 있기 때문에 이를 피하기 위해 n번째의 min/max값을 이용하거나 KL divergence를 최소화 하는 방식을 이용하거나 다양한 방식을 사용한다.
D. Range Calibration Algorithms: Static vs Dynamic
$\alpha$와 $\beta$를 정하는 과정을 input에 따라 정적으로 하냐(static) 동적으로 하냐(dynamic)의 차이가 있다. static한 방식은 input에 상관없이 미리 clipping range를 정하고 quantization이 진행된다면 dynamic은 input에 따라 다르게 clipping range가 정해진다. 따라서 inference 과정에서 clipping range를 정하고 quantization을 진행하는 dynamic 방식은 static 방식에 비해 높은 accuracy를 얻을 수 있지만 그만큼 연산에서 overhead가 존재한다.
따라서 overhead가 없는 static한 방식으로 inference전에 미리 clipping range를 구하는 방법이 연구가 많이 되었는데 calibration용 input을 만들어 미리 typical range를 구해서 적용하는 방식이나 training과정에서 정하는 방법 등이 있다. 여기서 Mean Squared Error(MSE)나 다양한 방식이 적용되곤 한다. 관련된 연구들로 LQNets, PACT, LSQ, LSQ+ 등의 연구가 있다.
E. Quantizaion Granularity

Quantization의 range를 정할 때 모든 filter의 range를 같게 만들 수도 있고 layer별로 다르게 할 수도 있고 다양하게 적용이 가능하다.
Layerwise Quantizaion : layer 별로 range를 정하는 방법
Groupwise Quantizaion : 한 layer 안에 있는 여러 filter들을 묶어 range를 정하는 방법
Channelwise Quantizaion : 가장 많이 쓰이는 방법이고 channel 별로 다르게 range를 정하는 방법
Sub-channelwise Quantizaion : 하나의 filter 안에서도 각 parameter별로 묶어 range를 정하는 방법. overhead가 가장 크나 가장 정확도는 높은 방법이다.
F. Non-Uniform Quantizaion

위의 그림의 오른쪽 처럼 r 값을 일정하게 나누어 quantization을 하는 것이 아니라 범위를 다양하게 나누어 quantizaion을 적용하는 방법이다. log scale로 나눠서 logarithmic dstribution을 적용해서 exponential하게 구간을 나누는 방법이 많이 쓰인다.
또한 r 값을 binary vector의 합으로 표현해서 binary code based quantizaion 방식도 많이 쓰이는데 아래와 같은 식으로 표현이 가능하다.

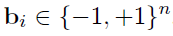

최근 work들에서는 이러한 quantization 방식을 하나의 optimization 방식으로 보고 아래와 같은 식으로 만들어 quantization 된 값과 이전 값을 최대한 유사하게 만드는 방식으로 풀기도 한다고 한다.

또한 quantizer 자체를 learnable하게 만들어 푸는 방식, k-means를 이용하는 clustering 방식 등 quantization 하는 방법이 다양하게 존재한다.
Non-uniform 방식이 정보를 더 잘 표현하는 방식은 맞지만 computation 관점(CPU나 GPU에서 동작할 때)에서 효율적으로 적용하기 어려워 uniform quantization 방식을 많이 사용한다고 한다.
G. Fine-tuning Methods (QAT, PTQ, Zero-shot)
pre-trained 된 model이 있고 그 모델에 quantization을 적용하면 일정 부분 정확도에 손실이 온다. 따라서 이를 해결하기 위해 quantization 이후 재 학습을 시켜 정확도를 복원하는 과정이 있고 (Quantization Aware Training (QAT)) 재 학습 없이 그대로 사용하는 방식도 있다. (Post Training Quantization (PTQ)).
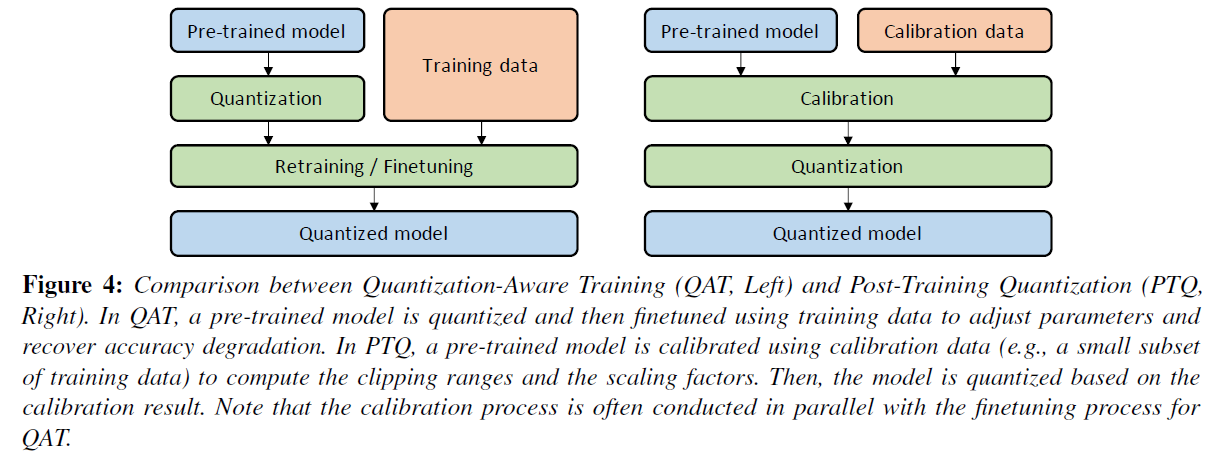
위의 그림의 왼쪽에서는 training data를 이용하여 quantization 이후 재 학습하는 과정이 있고(QAT) 오른쪽에서는 Calibration data만을 이용하여 model을 quantization하고 바로 사용한다(PTQ).
Quantization 된 모델을 재 학습 시킬 때(QAT방식에서) back propagation에서 주의해야할 점이 있다. 아래 그림에서 보이는 것처럼 Quantization 식이 미분가능하지 않으므로 backward 연산이 진행이 안될 수 있다는 점인데 이를 해결하기 위해 Straight Through Estimator (STE) 방식을 많이 사용한다.

기존의 방식대로 미분해서 backward 연산을 적용하면 quantizer에서 모두 기울기가 0이 되어버려서 backward 연산이 진행이 되지 않는다. 대신 STE (단순이 identity function이다) 를 적용해 backward 연산에 대신 사용해준다. 굉장히 잘 작동하는 방법이라고 한다.
주로 STE를 사용하긴 하지만 대체제로 stochastic neuron 방법을 적용하기도 하고 아예 Quantizer로 다른 regluarization operator를 사용하여 미분가능한 형태로 만들어 적용하기도 한다(Non-STE). 하지만 튜닝이 많이 필요해 간단하고 효과가 좋은 STE 방식을 많이 사용한다고 한다.
QAT 방식으로는 PACT, QIT, LSQ, LSQ+ 등의 연구가 있고
PTQ 방식으로는 ACIQ(channel wise로 quantization), OMSE(quantization이 적용된 tensor와 원래 값의 L2 distance 최소화), OCS(outlier 값을 가진 channel을 특별 처리) , AdaRound(기존의 navie 한 round-to-nearest 방법 대신 adaptive rounding method를 새로 제시, 변화량이 +-1 안에서 처리되도록 만듦) 등의 연구가 있다.
당연히 PTQ 방식이 resource도 적게 필요하고 재 학습을 할 필요가 없다는 장점이 있지만 정확도는 QAT가 더 높다.
마지막으로 Zero-shot으로 quantization을 적용하는 방법(ZSQ) 이 있다. 이 때, 두가지 경우로 나눌 수 있는데
Level 1: ZSQ + PTQ : 데이터가 없고 finetuning도 하지 않는다.
Level 2: ZSQ + QAT : 데이터가 없지만 finetuning을 한다.
Level 2 방법을 적용하기 위해 finetuning용 synthetic data를 만드는 과정이 있는데 pretrained model을 discriminator로 이용해 gan을 만들어 이용하는 방법이 있다.

1. random으로 생성된 이미지를 pretrained-model에 넣고 아웃풋의 결과가 argmax로 one hot vector로 만들었을 때와 비슷해지도록 loss 설정
2. 실제 이미지는 activation의 값이 큼, pretrained-model의 activation을 크게 만들기
3. 여러 class가 균일하게 나오도록 loss 설정
이런 방식으로 pretrained 모델만 가지고 synthetic data를 만들어 QAT에 활용하는 방법이 존재한다.
H. Stochastic Quantization
QAT에서 weight update 양이 너무 적으면 quantization에서 변화량이 사라져 버려서 학습이 멈추는 현상 발생한다. 따라서 weight update를 아래의 식처럼 stochastic으로 바꿔 update한다고 한다.

이외에도 QuantNoise에서는 일부 weight만 subset으로 만들어 update 해주는 등의 방법을 사용한다. 하지만 이러한 stochastic 방법은 Random number 생성에 overhead커서 주로 사용되지는 않는다고 한다.
여기까지 이 논문에서 다룬 Basic concept 내용이고 분량 상 다음 포스팅에서 Advanced concept 내용을 다루고자 한다.

