https://www.youtube.com/@MITHANLab
MIT HAN Lab
MIT HAN Lab: Hardware, AI and Neural-nets Accelerate Deep Learning Computing Group website: hanlab.mit.edu TinyML Project: tinyml.mit.edu TinyML Course: efficientml.ai, streamed via live.efficientml.ai every Tuesday/Thursday 3:35-5:00pm ET, fall 2022.
www.youtube.com
2022년 가을학기에 MIT에서 열린 Song Han 교수님의 TinyML and Efficient Deep Learning Computing 강의이다. 중요한 내용들만 골라 요약하는 식으로 글을 써보려고 한다.
Introduction to Pruning

Lecture 3에서는 네트워크 압축(compression) 기법 중 가장 많이 쓰이는 방법중 하나인 pruning에 대한 설명을 한다. pruning이란 말 그대로 위의 그림처럼 네트워크의 수많을 연결들을 가지치기를 하는 것이다.
이러한 pruning을 적용하는 방법은 굉장히 다양하다. Neural network는 weight, weight들이 모여있는 filter, filter들이 모여있는 Layer, Layer들이 모여있는 Block 등등 다양하게 group을 만들수 있고 각 group마다 다르게 pruning을 적용할 수 있고 pruning을 진행할 때 어떤 연결을 어떤 기준으로 없앨 것이냐 또한 중요한 문제이다.
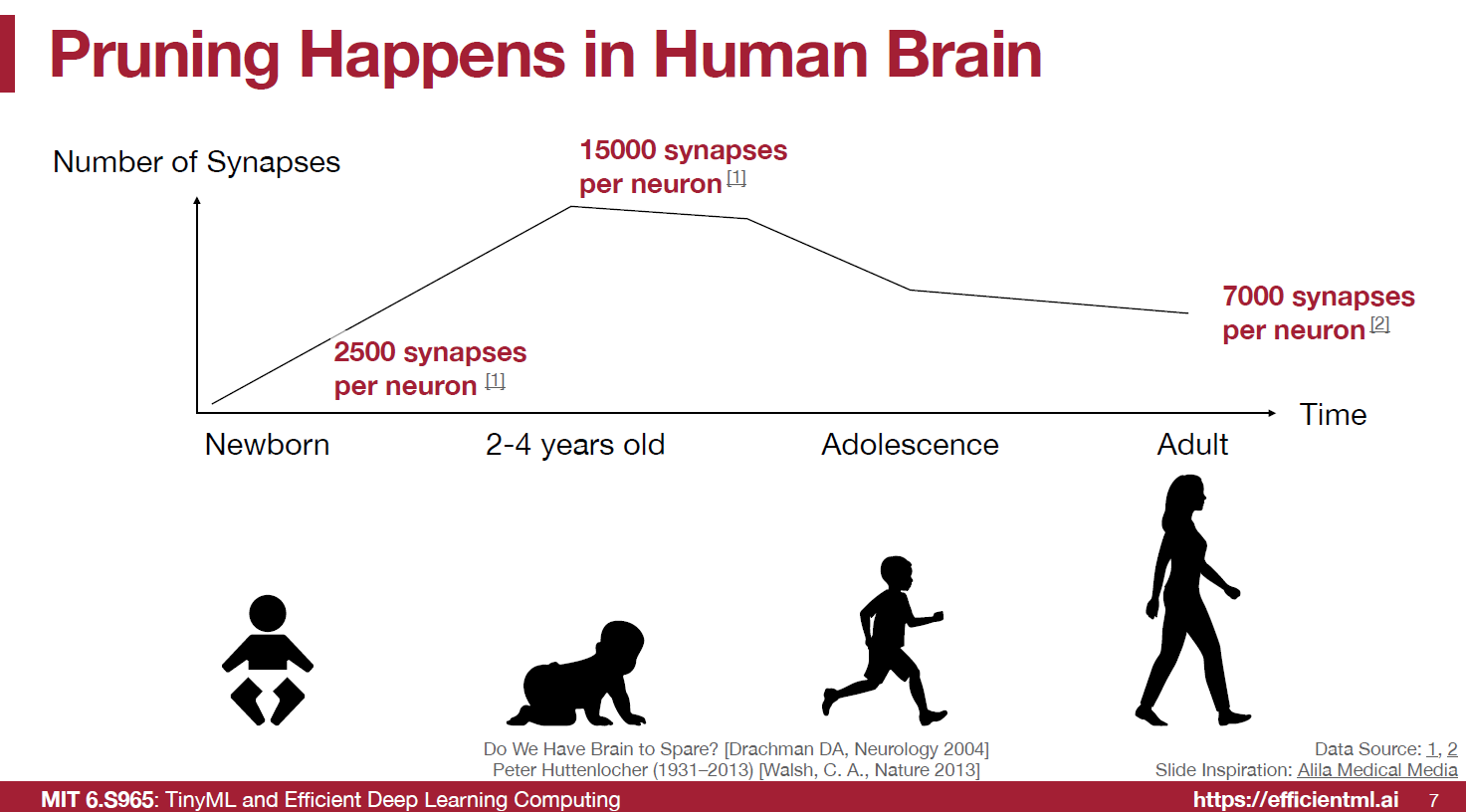
pruning은 인간의 뇌에서도 자연적으로 일어나는 현상이라고 한다. 뉴런당 연결되어 있는 synapse 수가 어른이 되면서 위의 그림처럼 작아진다고 한다.

기본적인 pruning을 하는 순서는
1. 원래 네트워크를 학습한다.
2. 불필요한 네트워크를 pruning한다.
3. pruning된 네트워크를 재학습을 한다.(finetuning)
이러한 순서이다.
위의 그림처럼 pruning만 했을 때는 정확도가 금방 떨어지고 pruning이후 finetuning 과정까지 거치면 약 80% 까지 parameter를 pruning해도 정확도가 떨어지지 않았다. 추가로 위의 순서에서 2,3번을 training 과정 중간에 넣어서 계속 반복하는 방법을 iterative pruning이라고 하는데 이러한 iterative pruning 방법을 적용하면 90%까지 parameter를 줄여도 성능이 떨어지지 않았다고 한다.
How should we formulate pruning?

기본적으로 pruning은 위의 그림처럼 formulation할 수 있다. Loss를 최소화 하면서도 Weight의 개수를 특정 개수 이하로 줄이는 것이다.
Pruning Granularity
위에서 언급했듯이 pruning을 하는 방법이 되게 다양한데 그중 granularity를 다르게 하는 방법들이다.
먼저 convolution layer가 있고 그러한 layer tensor의 shape을 [O, I, K, K] 라고 하자. 각각 O는 output feature map의 개수고 I는 input feature map의 개수, K는 filter의 kernel size이다.

위의 3x3 convolution filter가 모여있는 layer를 생각해보자. 그러면 layer의 tensor shape은 [O, I, 3, 3]이 될 것이다.
그림의 가장 왼쪽처럼 filter에서 weight들을 각각 규칙성 없이 pruning을 할 수도 있다. 그 오른쪽으로 가면 특정 pattern 대로 weight들을 pruning할수도 있고 vector-level로 pruning하면 가운데 그림처럼 3x3 matrix의 row대로 잘라서 pruning을 할수도 있다. 여기까지는 각 3x3 matrix 안에서 pruning을 한다.
이제 kernel-level pruning을 하면 3x3 filter들을 통채로 pruning할 수도 있다. 3x3 filter가 Output * input 개수만큼 있는데 그 중에서 선택할 filter를 고른다고 생각하면 된다.
channel-level pruning을 하면 output을 줄인다는 얘기인데 위에서 얘기했듯이 layer의 tensor shape은 [O, I, 3, 3]으로 즉 [I, 3, 3] shape의 텐서가 Output 개수만큼 있는데 그 중에서 사용할 channel을 고른다는 이야기이다.

위에서 얘기한 방식들은 모두 각각 장단점이 있다. irregular한 방식으로 pruning을 하게 될 경우 (Fine -grained / Unstructured) pruning을 더욱 flexible하게 할 수 있다. 그래서 똑같은 weight개수를 줄이면 regular하게 pruning을 했을 때보다 정확도는 높을 수 있다. 하지만 accelerate에는 좋지 않다. 보통 gpu에서 matrix 연산들은 묶여서 한번에 진행되는데 matrix안에서 특정 값이 0이여도 다른 값을 계산하는 동안 어차피 기다려야하거나 0의 multiplication 연산을 skip하는 특별한 library나 hardware 설계가 없으면 큰 속도차이가 없을 수 있다.
반면, coase-grained/sturctured pruning을 진행하는 경우 weight들이 묶여서 pruning되기 때문에 조금 덜 flexible하게 선택을 하게 되지만 accelerate에 용이하다는 장점이 있다. 직관적으로 위에서 kernel pruning이나 channel pruning은 애초에 특정 filter들의 연산자체를 안하게 만들면 되기 때문에 줄이는 만큼 속도가 상승한다.
irregular한 방법으로 pruning을 했을 때 accelearte하는 방법에 대해 간단히 설명하면 아래와 같다.

N:M sparsity는 M개를 pruning하면 그중에 메모리가 contiguous하게 연결되어 있는 값들이 N개 있는 것이다. 위의 그림에서 보이듯 2:4 sparsity matrix같은 경우는 compressed matrix를 만들어 연산해서 2x speed up을 해주는 기능을 제공하는 gpu도 있다고 한다.
Pruning Criterion
이제 pruning을 어떤 기준으로 할지에 대해 생각해보자.
먼저 가장 기본적인 방법으로 weight의 절댓값을 가지고 pruning을 하는 방법이다. magnitude-based pruning 방식으로 기본적으로 가장 많이 쓰이는 방법이면서 굉장히 간단하다. 단순 절댓값을 사용할 수도 있고 row별로 절댓값의 합을 사용해 raw 별로 pruning을 할수도 있고 제곱을 더한값에 루트를 씌우는 L2-norm을 이용할수도 있고 등등 다양하지만 비슷비슷한 방법들이 많이 있다. 기본적으로 전제는 절댓값이 큰 weight가 더 중요하다는 것이다. 아래에 예시들이 있다.



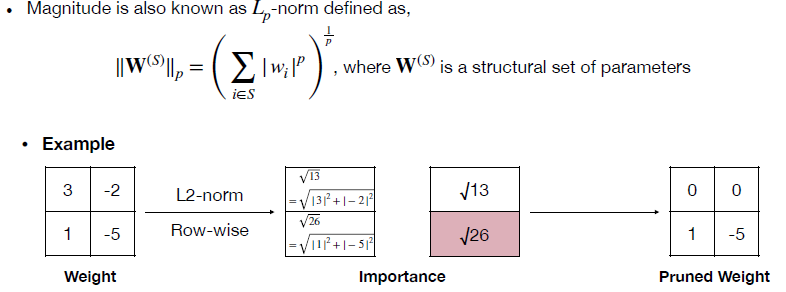
기본적으로 위의 예시들은 모두 fine-grained 방식의 pruning으로 예시가 들어져 있지만 2x2 filter가 많이 있는 상황이라면 weight의 절댓값들을 모두 합한 값들을 각 filter의 중요도로 평가해서 이러한 magnitude based 방법으로 filter pruning도 진행할 수 있다.
filter pruning을 하는 방식에는 위에서 얘기한 weight의 magnitude를 이용하는 방법외에도 굉장히 다양하다. 밑의 그림은 trainable한 scailing factor를 만들어 filter pruning에 사용하는 방식이다.

또한 Taylor Expansion을 이용해 weight의 중요도를 측정하는 방법도 있다. 기본적으로 모든 network의 목적은 loss 값을 줄이는 것이고 특정 weight가 없어졌을 때 loss가 얼마나 변화하는지를 보면 특정 weight의 중요도를 알 수 있을 것이다. 이를 weight 하나 하나 모두 제거해가며 측정할 수는 없기 때문에 아래와 같은 taylor expansion을 이용해 approximation을 통해 값을 얻어낸다.

위의 식에서 몇가지 가정을 넣어 term을 조금 더 없애 simplify할 수 있다.
먼저 2차항을 살리는 second-order-based pruning 방법이다.

가정 1. Loss function은 대부분 quadratic이므로 식의 가장 오른쪽에 있는 3차항 부터는 안써도 괜찮다.
가정 2. training이 끝난 netowrk의 경우 loss 값의 gradient는 거의 0에 가깝기 때문에 gradinet*weight인 1차항은 안써도 괜찮다.
가정 3. 각각의 weight가 loss에 주는 영향은 independt이므로 둘이 곱하는 h*wi*wj 값 또한 안써도 괜찮다.
이 세개의 가정으로 각각 세개의 항을 없애주면 위의 그림의 아래처럼 loss를 weight로 두번 미분한 값에 weight의 제곱을 곱한값 하나만 남는다. 이러한 방식이 second-order-based pruning이 된다.
First-order-based pruning은 그냥 단순하게 taylor first order approximation 방법만 사용하는 것이다. 위에서 삭제한 1차항만 계산에 사용하는 방법이다. gradient*weight로 계산할 수도 있고 (gradient*weigt)^2으로 사용할수도 있고 filter에 있는 모든 weight들의 importance를 이같은 방식으로 계산해서 더해준다음 filter의 importance를 정해 filter pruning에도 적용할 수 있다.

단순 weight의 gradient값은 loss backward 연산이면 얻어지기 때문에 First-order-based pruning은 훨씬 연산이 간단하고 Second-order-based pruning은 loss를 weight로 두번 미분하는 값을 얻기가 조금 까다로워 연산이 조금 더 복잡하다.
또 다른 방법을 activation 이후의 값에서 zero activation의 비율을 따져서 pruning하는 방법인 APoZ도 있고 위에서 얘기한 First-order-based pruning을 activation 이후에 값에 적용시켜서 pruning을 하는 방법도 있다.


마지막으로는 layer의 output의 reconstruction error를 최소화 하는 방식이다. 아래 그림처럼 multiplication할 채널을 선택해서 원래 layer output과 pruning된 layer의 output을 비교해서 차이를 최소화 하는 방식이다. 이 방식에도 여러 방식이 있는데 greedy search 방법으로 특정 채널의 output의 L2 norm이 가장 작은순서대로 pruning을 하는 방법도 있고lease squares approach 방식을 쓰는 방법 등등 다양하게 있다.



뒤이어 part2 부분도 포스팅할 예정인데 Part2 강의에서는 pruning ratio를 어떻게 정해야하는지, fine-tuning 기법들 등에 대해 다룬다. 더 자세한 내용이 궁금한 사람들은 직접 유튜브에 들어가서 강의를 보면 좋을 것 같다.
'AI 강의 정리 > TinyML and Efficient Deep Learning' 카테고리의 다른 글
| Neural Architecture Search (NAS) - Once-for-All (0) | 2023.06.26 |
|---|---|
| Neural Architecture Search (NAS) - Hardware-Aware NAS (ProxylessNAS) (0) | 2023.06.22 |
| Neural Architecture Search (NAS) - Framework (0) | 2023.06.17 |
| Neural Architecture Search (NAS) - Manually Designed Neural Networks (0) | 2023.06.16 |



